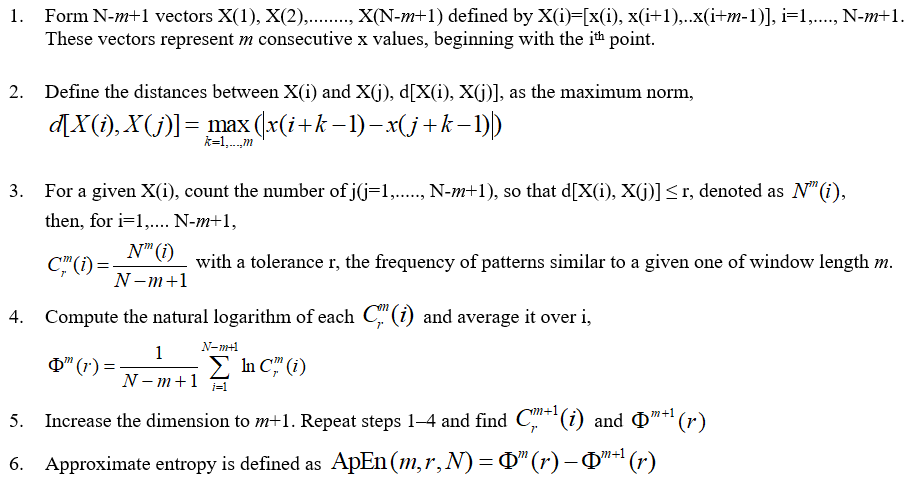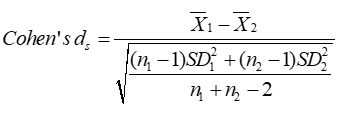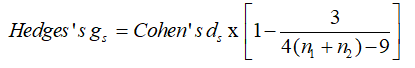Abstract
Introduction: Approximate Entropy (ApEn) is a widely enforced metric to evaluate the chaotic response and irregularities of RR intervals from an electrocardiogram. We applied the metric to estimate these responses in subjects with type 1 diabetes mellitus (DM1). So far, as a technique it has one key problem – the accurate choices of the tolerance (r) and embedding dimension (M). So, we attempted to overcome this drawback by applying different groupings to detect the optimum.
Methods: We studied 46 subjects split into two equal groups: DM1 and control. To evaluate autonomic modulation the heart rate was measured for 30 min in a supine position without any physical, sensory, or pharmacological stimuli. For the time-series, the ApEn was applied with set values for r (0.1→0.5 in intervals of 0.1) and M (1→5 in intervals of 1) and the differences between the two groups and their effect size by two measures (Cohen’s ds and Hedges’s gs) were computed.
Results: The highest value of statistical significance accomplished for the effect sizes (ES) for any of the combinations performed was -0.7137 for Cohen’s ds and -0.7015 for Hedges’s gs with M = 2 and r = 0.08.
Conclusion: ApEn was able to identify the reduction in chaotic response in DM1 subjects. Still, ApEn is relatively unreliable as a mathematical marker to determine this.
Keywords
diabetes mellitus, approximate entropy, tolerance, embedding dimension, HRV
Abbreviations
ApEn: approximate entropy; DM1: type 1 diabetes mellitus; r: tolerance; M: embedding dimension; ES: effect sizes; HRV: heart rate variability; ANS: autonomic nervous system; N: signal length
Introduction
The rhythm of RR intervals derived from an electrocardiographic trace can vary in an irregular and frequently chaotic manner [1]. Time-series analysis has encouraged researchers to study this area [2, 3]. Heart rate variability (HRV) is a simple, reliable and inexpensive method of monitoring the autonomic nervous system (ANS) and an important technique for assessing health and disease conditions [4–6]. Other approaches are either insensitive e.g., sympathetic skin response [7, 8] or too intricate and expensive as with quantitative pupillography [9]. Chaotic behavior in biological and medical dynamical systems may indicate normal physiological status, whereas loss of chaotic tendencies could be an abnormality marker [10, 11].
HRV can be assessed using approximate entropy (ApEn), as described in 1991 by Pincus [12]. The advantages of ApEn include low computational processor demand as it can adapt to small sample lengths (RR < 50) thus, it can potentially be applied online as in clinics and hospital units. Additionally, it can decipher information accurately in the presence of substantial noise. Yet, a key disadvantage of the technique is that it is very dependent on the parameter choices for tolerance (r) and embedding dimension (M). This makes the results from ApEn especially difficult to interpret and unreliable.
Here, in this study we systematically applied different combinations of r and M in subjects with and without type 1 diabetes mellitus (DM1). It is the aim that if we apply these combinations for these two parameters, we should acquire the optimal grouping which achieves the greatest statistical significances to discriminate between these two groups. The values we set for r (0.1→0.5) and M (1→5).
Methods
Patient selection and assessment
This study included 46 adults regardless of gender split equally into two groups. An experimental group DM1: male (44%) and a control group: male (65%). The inclusion conditions adopted were absence of cardio-respiratory diseases and pharmacotherapies; non-tobacco smokers and those who infrequently drink alcoholic beverages. These factors could influence the cardiac autonomic activity. Those subjects who satisfied the inclusion criteria were given an explanation of the objectives and procedures of the study and signed a confidential informed consent form. All the procedures used in this study were approved by the Research Ethics Committee of the Institution (Protocol No. 47/2011). The experimental protocol included two steps: identification and autonomic evaluation. During the identification, details were taken concerning the subjects’ medical history to determine whether they fulfilled the inclusion criteria and to characterize the population. The physical evaluation was performed by measurement of HRV.
Evaluations were conducted in a noiseless room with a temperature 23.87 ± 2.54°C and humidity 54.22 ± 8.51%. Movement inside the room and noises outside were regulated. All evaluations were undertaken in the afternoon, between 13:00 and 17:00, to circumvent circadian rhythm influence [13].
Demographic information regarding age, gender, signs and symptoms resulting from DM1, pharmacotherapies, associated pathologies, tobacco smoking, regular drinkers of alcoholic beverages and the level of physical activity measured by International Physical Activity Questionnaires (IPAQ) [14, 15], were obtained from the subjects.
The HRV evaluations were completed to authenticate the autonomic modulation and subjects were instructed to avoid alcoholic and/or ANS stimulants, for a period of 24 h before the evaluation. During the autonomic evaluation, the subjects were instructed to remain alert, silently, with spontaneous breathing resting in the supine position for 30 min on a sofa. After receiving an explanation of the data collection procedures, an electrode was located on the subjects’ chest, and the heart rate receiver (Polar Electro, model S810i, Finland) was attached to the subjects’ wrist. The apparatus had been previously validated to record beat-to-beat heart rate and for use in collecting HRV data for
analysis [6]. To analyze HRV indexes, exactly 1000 RR intervals were selected, then after digital and manual filtering to eliminate artifact and ectopic beats only series with greater than 95% of sinus beats were used in the protocol.
Mathematical Analysis
Approximate entropy (ApEn)
Entropy-based techniques are routinely involved in medical data analysis. ApEn is a process that assesses the level of regularity and the unpredictability of changes over time-series [16, 17]. ApEn is the logarithmic ratio of component-wise matching sequences from the signal length (N). Additional parameters include r and M. For instance, with studies assessing HRV in obese children [18], r is set to 0.2 and this represents 0.2 (or, 20%) of the standard deviation of the dataset of RR intervals. A value of zero for ApEn would indicate a totally predictable series. ApEn increases with increasing chaotic response and irregularities. ApEn is described algorithmically as follows. Given N data points from a time-series [x(n)] = x(1), x(2),…..x(N), one should follow these steps to compute ApEn:
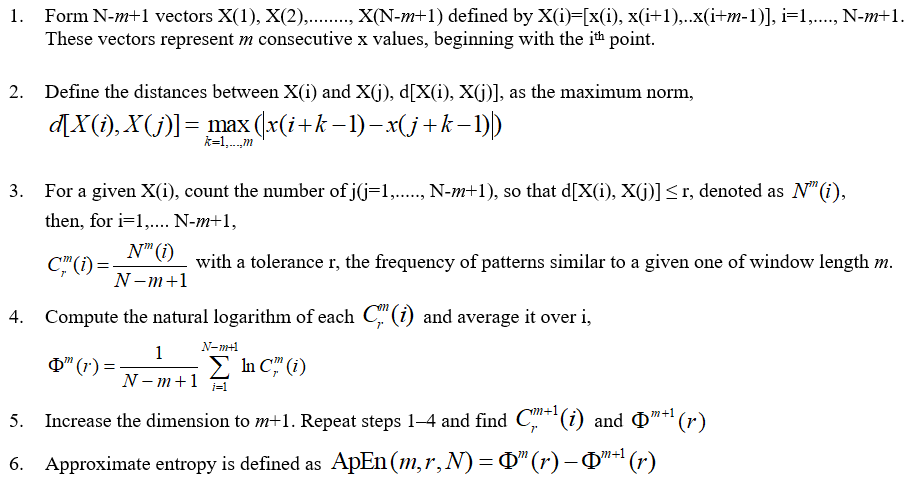
Effect sizes: Cohen’s ds and Hedges’s gs
We applied the effect sizes (ES) to assess the significance of the data. We did not evaluate normality and apply the one-way analysis of variance, or Kruskal-Wallis test as in previous studies [10, 19]. These two statistical tests cannot discriminate sufficiently between the small changes in significance that are apparent here.
Cohen’s ds is the leading subcategory of ES [20]. It refers to the standardized mean difference between two groups of independent observations for the appropriate sample. It is based on the sample means and gives a biased estimate of the effect size. In the algebraic formula for Cohen’s ds, the numerator is the variation between the means of two groups of observations. The denominator is the pooled standard deviation. These differences are squared. Then, they are summed and divided by the number of observations minus one for bias, referred to as Bessel’s correction, in the estimate of the variance. To conclude, the square root is applied to the denominator.
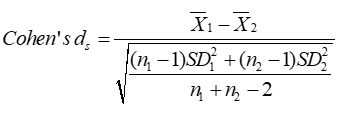
Hedges’s gs is an alternative and unbiased [21]. The difference between Cohen’s ds and Hedges’s gs is small especially in sample sizes (n > 20). We apply two ES here to check that the magnitude of the values coincides. The same subscript letter in Hedges’s gs is applied to distinguish the different calculations as was the case here for Cohen’s ds.
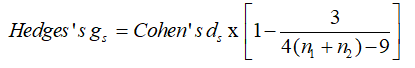
For the ES the Cohen’s ds and Hedges’s gs extents are designated as 0.01 > very small effect; 0.20 > small effect; 0.50 > medium effect; 0.80 > large effect. These are the benchmarks from Cohen [20] and, Sawilowsky [22].
Results
When ApEn is systematically applied to 25 suitably different parameters for r and M, just 40% of these combinations were suitable when considered physiologically (Figure 1 and 2). Chaos and irregularities usually decrease in pathological states. ApEn for controls and DM1 subjects with values for r (0.1→0.5 in intervals of 0.1) and M (1→5 in intervals of 1) are illustrated (Table 1).
As M increases the level of r is less critical. At M = 1.0, none of the values for r are suitable as DM1 has greater chaotic response than the control with positive ES. This is physiologically incorrect. At M = 2.0, r = 0.1 this is significant and physiologically appropriate. At that point, as M increases additional values for r become appropriate with negative ES. When M = 5.0, only r = 0.5 is physiologically unsuitable.
Moreover, as the M approaches 5.0 those values that are physiologically pertinent have reduced ES by both measures. When M = 2.0, r = 0.1 the ES by Cohen’s ds and Hedges’s gs are similar wherein their ES = -0.5700 and -0.5603, respectively (medium effect size). As M→5.0 these values decrease to ES = -0.0133 and -0.0131, correspondingly (very small effect size). When examining the results, (Table 1) we detect that the optimal combination of M is 4.0 and r is 0.1 with ES = -0.6928 and -0.6810 individually (medium effect size).
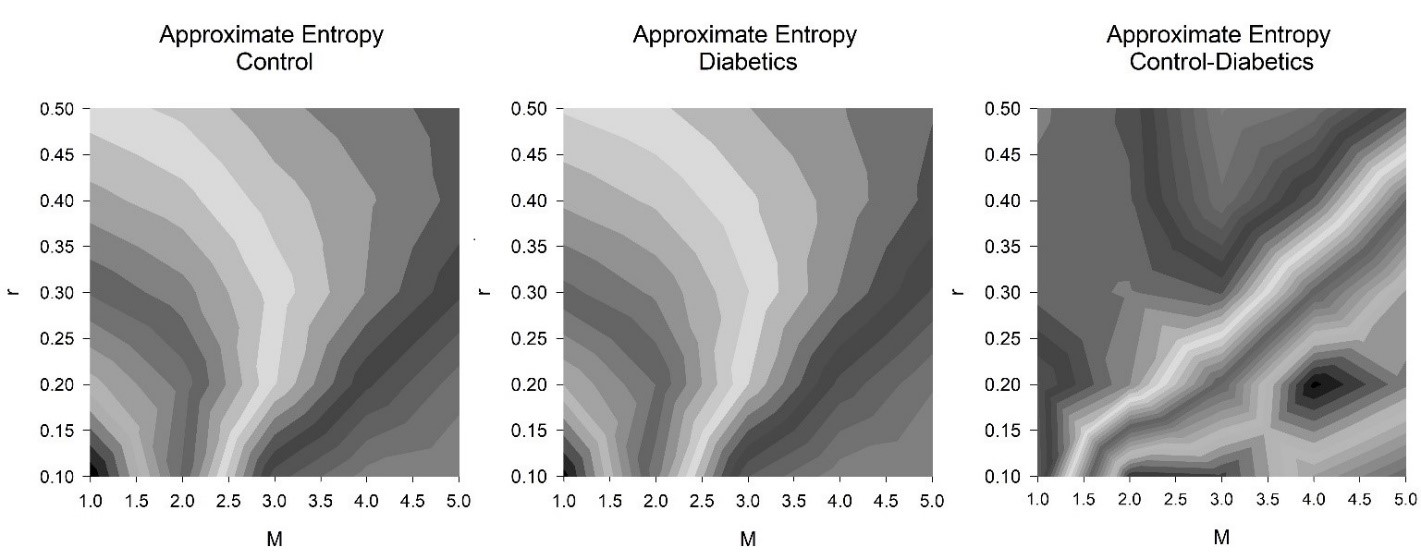
Figure 1: Contours greyscale, approximate entropy (ApEn) for controls and subjects with type 1 diabetes mellitus (DM1) (both n = 23). There were precisely 1000 RR intervals. Other parameters consist of tolerance (r) and, embedding dimension (M). There were 25 groups of values for tolerance (r) (0.1→0.5 in intervals of 0.1) and embedding dimension (M) (1→5 in intervals of 1), hence a grid of 5 by 5. The ApEn for the controls (left), those with DM1 (middle), the difference in ApEn between the controls and those with DM1 (right).
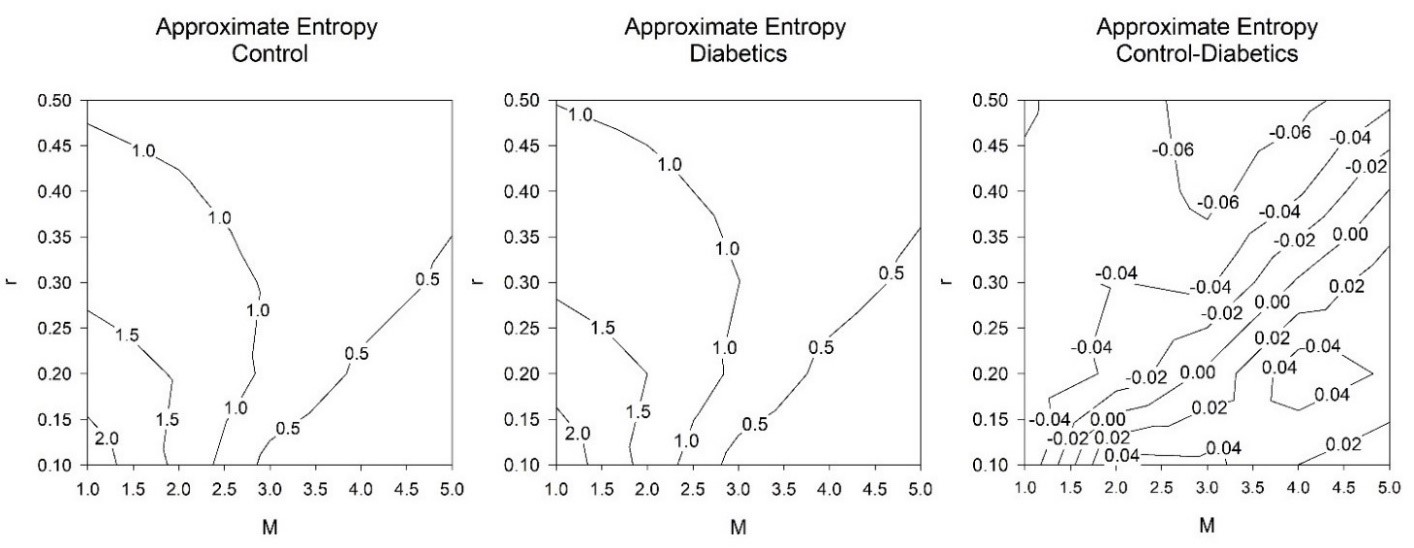
Figure 2: Contour lines, approximate entropy (ApEn) for controls and type 1 diabetes mellitus (DM1) subjects (both n = 23). There were exactly1000 RR intervals. Further parameters consist of tolerance (r) and, embedding dimension (M). There were 25 groups of values for tolerance (r) (0.1→0.5 in intervals of 0.1) and embedding dimension (M) (1→5 in intervals of 1), a grid of 5 by 5. The ApEn for the controls (left), those with DM1 (middle), the difference in ApEn between the controls and those with DM1 (right).
On closer examination, where the M values are fixed this can be surpassed. Studying in finer detail (Table 2) setting values of M and manipulating r. We set M = 2 and r = 0.01→0.23 in intervals of 0.01, hence 23 values of ApEn for the M of 2. Then, M = 3 and r = 0.01→0.23 in intervals of 0.01, hence a further 23 values of ApEn, and so on, until an M value of 5. For the combinations of M and r we determine that M = 2 achieves the most significance when r = 0.08. This then corresponds to ES = -0.7137 (Cohen’s ds) and -0.7015 (Hedges’s gs), thus medium ES with M = 2 and r = 0.08. This is the highest value of statistical significance achieved for any of the combinations presented in either Table 1 or 2.
Discussion
DM1 has been confirmed to be a dynamical disease which significantly reduces chaotic response. This has been observed using the chaotic global dimensions [10, 19] and the fractal dimensions, Higuchi and Katz [23]. We now study the responses of ApEn on exactly the same dataset as in the aforementioned studies. The results demonstrate that ApEn is able to identify the reduction in chaotic response and that the best combination of M and r for this were 2.0 and 0.08, respectively.
Measurement by ApEn has some advantages in that it can be applied to short time-series (RR < 50). Also, it is reasonable at responding accurately in the presence of considerable levels of noise. Still, its main disadvantage is the choice of optimal parameters for r and M. In this study, initially, we applied 25 different combinations of r and M. It was expected that since DM1 is a condition which lessens the chaotic response of HRV [10, 19, 23], those combinations of r and M which increase their responses for DM1 can be disregarded and they are physiologically incorrect. These provided positive ES for both Cohen’s ds and Hedges’s gs. 10 out of 25 (40%) of the permutations provided a higher value for the control than for the subjects with DM1. Therefore, less than half of the computations provided an accurate assessment. When scrutinizing the results further, we can observe that the optimum combination of M is 4.0 and r is 0.1 (Table 1). We now need to examine the values more closely regarding the r levels.
So, we fixed the values of M and inspected the values more closely regarding its tolerance, r (Table 2). r was initially set at 0.01 and increased up to 0.23 in equal units (0.01→0.23 at intervals of 0.01). Therefore, we computed 23 values for each value of M. The results for the two ES were similar. The highest level of discrimination for the appropriate physiological responses by Cohen’s ds and Hedges’s gs was ES = -0.7137 and -0.7015, respectively (medium effect size for M = 2.0 and r = 0.08). This exceeds the level of significance produced by M of 4.0 and r of 0.1 (Table 1) with ES = -0.6928 and -0.6810, correspondingly (medium effect size).
| M | r | Approximate entropy (n = 23) | Effect sizes (ES) |
| Mean control | ± SD control | Mean DM1 | ± SD DM1 | Cohen’s ds | Hedges’s gs |
| 1.0 | 0.1 | 2.2846 | 0.1646 | 2.3429 | 0.1256 | 0.3986 | 0.3917 |
| 1.0 | 0.2 | 1.7434 | 0.1738 | 1.7998 | 0.1433 | 0.3543 | 0.3482 |
| 1.0 | 0.3 | 1.3912 | 0.1705 | 1.4331 | 0.1576 | 0.2554 | 0.2510 |
| 1.0 | 0.4 | 1.1391 | 0.1623 | 1.1804 | 0.1538 | 0.2614 | 0.2569 |
| 1.0 | 0.5 | 0.9508 | 0.1547 | 0.9899 | 0.1474 | 0.2588 | 0.2544 |
| 2.0 | 0.1 | 1.3867 | 0.0479 | 1.3391 | 0.1080 | -0.5700 | -0.5603 |
| 2.0 | 0.2 | 1.4632 | 0.1152 | 1.4992 | 0.0980 | 0.3361 | 0.3303 |
| 2.0 | 0.3 | 1.2411 | 0.1377 | 1.2806 | 0.1439 | 0.2804 | 0.2756 |
| 2.0 | 0.4 | 1.0382 | 0.1378 | 1.0815 | 0.1442 | 0.3076 | 0.3024 |
| 2.0 | 0.5 | 0.8751 | 0.1307 | 0.9199 | 0.1425 | 0.3280 | 0.3224 |
| 3.0 | 0.1 | 0.3513 | 0.1053 | 0.3059 | 0.0989 | -0.4447 | -0.4371 |
| 3.0 | 0.2 | 0.9092 | 0.0774 | 0.9046 | 0.0800 | -0.0579 | -0.0569 |
| 3.0 | 0.3 | 0.9599 | 0.0824 | 1.0042 | 0.0634 | 0.6024 | 0.5921 |
| 3.0 | 0.4 | 0.8516 | 0.0887 | 0.9186 | 0.0959 | 0.7262 | 0.7138 |
| 3.0 | 0.5 | 0.7308 | 0.0853 | 0.8032 | 0.1065 | 0.7506 | 0.7377 |
| 4.0 | 0.1 | 0.0600 | 0.0333 | 0.0401 | 0.0233 | -0.6928 | -0.6810 |
| 4.0 | 0.2 | 0.4216 | 0.1028 | 0.3680 | 0.0947 | -0.5423 | -0.5330 |
| 4.0 | 0.3 | 0.6955 | 0.0665 | 0.6929 | 0.0682 | -0.0388 | -0.0382 |
| 4.0 | 0.4 | 0.7157 | 0.0693 | 0.7589 | 0.0581 | 0.6745 | 0.6630 |
| 4.0 | 0.5 | 0.6399 | 0.0739 | 0.7071 | 0.0823 | 0.8587 | 0.8440 |
| 5.0 | 0.1 | 0.0097 | 0.0097 | 0.0045 | 0.0055 | -0.6613 | -0.6500 |
| 5.0 | 0.2 | 0.1472 | 0.0695 | 0.1102 | 0.0495 | -0.6140 | -0.6035 |
| 5.0 | 0.3 | 0.4236 | 0.0858 | 0.3905 | 0.1078 | -0.3398 | -0.3339 |
| 5.0 | 0.4 | 0.5720 | 0.0604 | 0.5713 | 0.0537 | -0.0133 | -0.0131 |
| 5.0 | 0.5 | 0.5616 | 0.0625 | 0.6064 | 0.0550 | 0.7609 | 0.7479 |
Table 1: Approximate entropy (ApEn) for controls and type 1 diabetes mellitus (DM1) subjects (both n = 23). There were exactly 1000 RR intervals for each subject. Other parameters consist of tolerance (r) and, embedding dimension (M). There were 25 groups of values for tolerance (r) (0.1→0.5 in intervals of 0.1) and embedding dimension (M) (1→5 in intervals of 1). Illustrated are the ApEn for the mean controls with standard deviation, mean DM1 and standard deviation, then their effect sizes for control vs. DM1 by Cohen’s ds and Hedges’s gs.
Accordingly, in this study ApEn has been revealed to be a significant mathematical marker if M and r are chosen such that the differences are maximized as measured by Cohen’s ds and Hedges’s gs. There is currently no procedure or algorithm by which these values can be selected. So, ApEn can be viewed as an erratic mathematical marker which can only be used when M and r are usually selected by trial and error. Typically, for assessing HRV studies we set M = 2.0 and r = 0.2 where this is 20% of the standard deviation of the time series [18]. Consequently, if we were enforcing ApEn in a critical situation in clinics and hospital units it would be too time costly to calculate all the possible values of ApEn as it would require performing multiple calculations each time to achieve the precise value to assess the health and disease conditions.
Notwithstanding the advantages of ApEn, such as performing well on short time-series (RR < 50), even in the presence of noise in this study ApEn has been demonstrated to be a relatively unreliable mathematical marker. We encourage the use of the chaotic global techniques as alternative for assessing health and disease conditions in particular, or Katz’s fractal dimensions. Certainly, the chaotic globals are easier to enforce, perform well on relatively short time-series (RR > 256) [24], even with levels of noise, discriminate between the groups better and need less computational time such as is important in critical situations where slow mathematical responses to physiological variables could be life-threatening. Accordingly, they are better coordinated in situations that require quick response. The Katz’s fractal dimension metric is appropriate but necessitates cubic spline interpolation [23, 25] which can be time costly in situations where speed is important.
| r | Effect sizes (ES) by Cohen’s ds | Effect sizes (ES) by Hedges’s gs |
| M = 2 | M = 3 | M = 4 | M = 5 | M = 2 | M = 3 | M = 4 | M = 5 |
| 0.01 | 0.5912 | 0.3660 | 0.2949 | < 0.0001 | 0.5810 | 0.3597 | 0.2898 | < 0.0001 |
| 0.02 | -0.2741 | 0.0136 | 0.2175 | -0.2949 | -0.2694 | 0.0134 | 0.2138 | -0.2898 |
| 0.03 | -0.1014 | 0.1039 | 0.2489 | -0.2949 | -0.0997 | 0.1021 | 0.2446 | -0.2898 |
| 0.04 | -0.0581 | -0.0312 | 0.0815 | -0.3055 | -0.0571 | -0.0307 | 0.0801 | -0.3002 |
| 0.05 | -0.4777 | -0.1635 | -0.2148 | -0.3109 | -0.4695 | -0.1607 | -0.2111 | -0.3056 |
| 0.06 | -0.4884 | -0.2610 | -0.4455 | -0.3518 | -0.4800 | -0.2566 | -0.4379 | -0.3458 |
| 0.07 | -0.1427 | -0.1279 | -0.3659 | -0.1325 | -0.1403 | -0.1257 | -0.3596 | -0.1303 |
| 0.08 | -0.7137 | -0.5661 | -0.6981 | -0.6107 | -0.7015 | -0.5564 | -0.6862 | -0.6002 |
| 0.09 | -0.3542 | -0.2535 | -0.4365 | -0.4263 | -0.3481 | -0.2492 | -0.4290 | -0.4190 |
| 0.10 | -0.5700 | -0.4447 | -0.6928 | -0.6613 | -0.5603 | -0.4371 | -0.6810 | -0.6500 |
| 0.11 | -0.2413 | -0.2014 | -0.3365 | -0.4069 | -0.2371 | -0.1979 | -0.3308 | -0.3999 |
| 0.12 | -0.2473 | -0.1545 | -0.0882 | -0.1070 | -0.2430 | -0.1518 | -0.0867 | -0.1052 |
| 0.13 | -0.1262 | -0.1136 | -0.0826 | -0.1558 | -0.1240 | -0.1116 | -0.0811 | -0.1531 |
| 0.14 | -0.0201 | -0.1092 | -0.0699 | -0.1031 | -0.0198 | -0.1074 | -0.0687 | -0.1013 |
| 0.15 | -0.0297 | -0.1626 | -0.0984 | -0.1297 | -0.0292 | -0.1599 | -0.0968 | -0.1275 |
| 0.16 | 0.1054 | -0.3189 | -0.3353 | -0.3192 | 0.1036 | -0.3134 | -0.3296 | -0.3137 |
| 0.17 | 0.1932 | -0.1979 | -0.2789 | -0.2999 | 0.1899 | -0.1945 | -0.2741 | -0.2947 |
| 0.18 | 0.2201 | -0.2122 | -0.3394 | -0.3318 | 0.2163 | -0.2085 | -0.3335 | -0.3261 |
| 0.19 | 0.2662 | -0.1081 | -0.3939 | -0.4138 | 0.2616 | -0.1063 | -0.3872 | -0.4067 |
| 0.20 | 0.3361 | -0.0579 | -0.5423 | -0.6140 | 0.3303 | -0.0569 | -0.5330 | -0.6035 |
| 0.21 | 0.2771 | 0.1568 | -0.3548 | -0.4674 | 0.2723 | 0.1542 | -0.3488 | -0.4593 |
| 0.22 | 0.2819 | 0.1939 | -0.3274 | -0.4378 | 0.2770 | 0.1905 | -0.3218 | -0.4303 |
| 0.23 | 0.2883 | 0.2861 | -0.2598 | -0.4198 | 0.2834 | 0.2812 | -0.2553 | -0.4126 |
Table 2: Effect Sizes (ES) by Cohen’s ds and Hedges’s gs for controls vs. type 1 diabetes mellitus (DM1) subjects (both n = 23). Exactly 1000 RR intervals were necessary in the calculations for each subject. Other parameters consist of tolerance (r) and embedding dimension (M) which is fixed at 2, 3, 4, and 5. There were 23 groups of values for tolerance (r) (0.01→0.23 in intervals of 0.01).
Conclusion
DM1 has been established as a dynamical disease which reduces chaotic response. In this study, ApEn was able to identify the reduction in chaotic response in DM1 and the best combination of M and r for this were 2.0 and 0.08, respectively. Limitations of the study include the small sample size and the variability in the HRV. Thus far, ApEn has been demonstrated to be a relatively unreliable mathematical marker.
Conflicts of Interests
The authors declare no conflict of interests regarding the publication of this article.
Funding Statement
Financial support was provided by CNPq – number process: 477442/2012-9.
References
- Goldberger AL. Cardiac chaos. Science. 1989;243(4897):1419.
- Ho M-W. The rainbow and the worm: The physics of organisms. Singapore: World scientific; 2008.
- Prigogine I. Non-equilibrium statistical mechanics. New York: Interscience; 1962.
- Mackey MC, Milton JG. Dynamical diseases. Ann N Y Acad Sci. 1987;504(1):16-32.
- Chang S. Physiological rhythms, dynamical diseases and acupuncture. Chin J Physiol. 2010;53(2):77-90.
- Vanderlei LC, Silva RA, Pastre CM, et al. Comparison of the polar S810i monitor and the ECG for the analysis of heart rate variability in the time and frequency domains. Braz J Med Biol Res. 2008;41(10):854-59.
- Rachow T, Berger S, Boettger MK, et al. Nonlinear relationship between electrodermal activity and heart rate variability in patients with acute schizophrenia. Psychophysiology. 2011;48(10):1323-32.
- Wiertel-Krawczuk A, Hirschfeld AS, Huber J, et al. Sympathetic skin response following single and combined sound and electrical stimuli in young healthy subjects. J Med Sci. 2016;85(2):106-13.
- Baum P, Petroff D, Classen J, et al. Dysfunction of autonomic nervous system in childhood obesity: a cross-sectional study. PLoS One. 2013;8(1):e54546.
- De Souza NM, Vanderlei LCM, Garner DM. Risk evaluation of diabetes mellitus by relation of chaotic globals to HRV. Complexity. 2015;20(3):84-92.
- Bernardo AF, Vanderlei LC, Garner DM. HRV Analysis: A Clinical and Diagnostic Tool in Chronic Obstructive Pulmonary Disease. Int Sch Res Notices. 2014;2014:673232.
- Pincus SM. Approximate entropy as a measure of system complexity. Proc Natl Acad Sci USA. 1991;88(6):2297-301.
- Armstrong RG, Kenny GP, Green G, et al. Diurnal variation in heart rate variability before and after maximal exercise testing. Chronobiol Int. 2011;28(4):344-51.
- Rzewnicki R, Auweele YV, Bourdeaudhuij ID. Addressing overreporting on the International Physical Activity Questionnaire (IPAQ) telephone survey with a population sample. Public Health nutr. 2003;6(3):299-305.
- Hallal PC, Gomez LF, Parra DC, et al. Lessons learned after 10 years of IPAQ use in Brazil and Colombia. J Phys Act Health. 2010;7 (Suppl 2):S259-64.
- Pincus S. Approximate entropy (ApEn) as a complexity measure. Chaos. 1995;5(1):110-17.
- Richman JS, Moorman JR. Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol Heart Circ Physiol. 2000;278(6):H2039-49.
- Vanderlei F, Vanderlei LCM, de Abreu LC, et al. Entropic analysis of HRV in obese children. Int Arch Med. 2015;8(2015)1-9.
- Garner DM, de Souza NM, Vanderlei LCM. Risk Assessment of Diabetes Mellitus by Chaotic Globals to Heart Rate Variability via Six Power Spectra. Rom J Diabetes Nutr Metab Dis. 2017;24(3):27-36.
- Cohen J. Statistical power analysis for the behavioral sciences. 2nd ed. New York: Routledge; 2013.
- Hedges LV, Olkin I. Statistical methods for meta-analysis: Academic press; 1985.
- Sawilowsky SS. New effect size rules of thumb. Journal of Modern Applied Statistical Methods. 2009;8(2): 597-99.
- Garner DM, de Souza NM, Vanderlei LCM. Heart Rate Variability Analysis: Higuchi and Katz’s Fractal Dimensions in Subjects with Type 1 Diabetes Mellitus. Rom J Diabetes Nutr Metab Dis. 2018;25(3):289-95.
- Garner DM, Vanderlei FM, Valenti VE, et al. Non-linear regulation of cardiac autonomic modulation in obese youths: interpolation of ultra-short time series. Cardiol Young. 2019;29(9):1196-1201.
- Kreyszig E. Advanced engineering mathematics. 8th ed. California: Wiley; 2011.