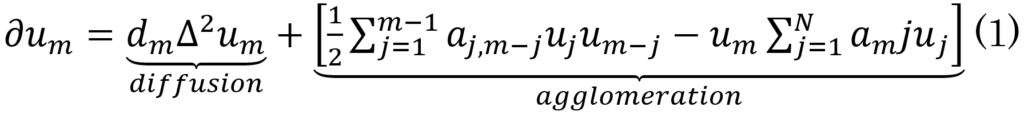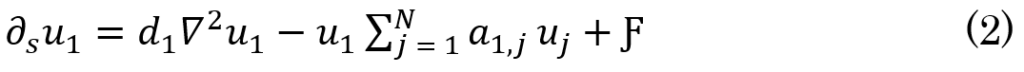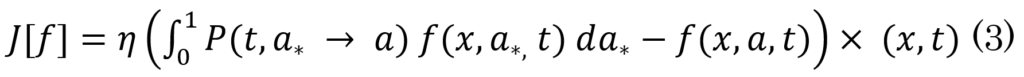Introduction: Several hypotheses explain the onset and pathology of Alzheimer’s disease (AD), such as the amyloid hypothesis and the tau hypothesis. Consequently, various biomarkers have been identified and drugs developed, but the fight against the AD epidemic is still ongoing. Perhaps it is time to explore new hypotheses. To begin with, researchers have shown that neuropathology associated with AD typically starts to develop decades before the clinical onset or manifestation of the disease. However, therapeutic interventions are still being designed to address mild-to-moderate stages of the disease, which are unfortunately irreversible.
Methods: We have reviewed various mathematical models to identify any missing parameters that could support the proposed time factor hypothesis for AD. In addition, we have developed a cognitive function algorithm that utilizes the identified parameters. The algorithm’s results are used to predict the likelihood of neuritic dystrophy.
Results: With mathematical evidence, we emphasize the importance of timely diagnosis of AD and provide support for considering an earlier age of 30 years (rather than 60 years or older) for effective interventions, including diagnosis and drug development.
Discussion: Among other points, we showed that Aβ₄₂ aggregation starts around age 30–40 years. With this information, we propose the need to re-engineer the concepts behind the science of AD. The number of AD patients will experience a nose dive if effort aimed at timely prevention of (for instance) Aβ₄₂ aggregation is expended.

Alzheimer’s disease, the time factor hypothesis, atrophy, neuropathology

AD: Alzheimer’s disease, APP: amyloid precursor protein, CSF: cerebrospinal fluid, GVD: granulovacuolar degeneration, NFTs: neurofibrillary tangles, CAT: computerized axial tomography, MRI: magnetic resonance imaging, PET: positron emission tomography, fMRI: functional magnetic resonance imaging

Alzheimer’s disease (AD) is the most prevalent neurodegenerative disorder and the leading cause of dementia in older adults; it accounts for about 80% of cases [1]. AD is an age-related disease in which degenerative brain disorder characterized by neuronal atrophy progresses over decades, destroying memory and cognitive decline. As well as behavioral, physical inabilities, and death [2, 3]. There are many schools of thought on the onset of AD. It has been observed that about 50–80% of AD cases are inherited [4], while other patients develop the disease even when they are not genetically susceptible to it [5]. Late-onset AD is due to the APOEϵ4 gene and three single-gene mutations, namely, amyloid precursor protein (APP) on chromosome 21, presenilin 1 (PSEN1) on chromosome 14, and presenilin 2 (PSEN2) on chromosome 1, that are 50% responsible for early onset of the disease [5].

Life expectancy in AD varies from 3–10 years depending on the age at which the patient was diagnosed [6, 7]. There has been a rising number of suicides associated with AD [8], recorded that over 95 patients of AD died by suicide in England (from January 1, 2001, through December 31, 2019). Perhaps this stems from the frustrations and concerns of AD having no cure. There are no clinical diagnostic tools for AD, and available mechanisms are inconclusive and autopsy-dependent. Unfortunately, current treatments aim to treat cognitive issues instead of underlying pathology [9]. This situation further exacerbates the severity of the disease, as it gives ample time for unlimited brain atrophy. The focus of this article is on developing a paradigm for the creation of diagnostic devices as a byproduct of mathematical models.

Mathematical models of AD provide a road map of the disease’s progression, highlighting key factors and interactions. It helps researchers navigate the complexities of AD and identify potential intervention targets. Just as a map can be used to plan a route, a mathematical model can be used to predict the effects of potential treatments or interventions. Researchers can explore different scenarios and evaluate the likely outcomes by simulating the model with different inputs.

Mathematical models also create entry points for the introduction of AI and machine learning algorithms to aid studies in biomarker discovery [10, 11]. Recently, neuroimaging has been employed as a diagnostic tool to determine whether or not there is beta-amyloid (or tau protein) in the brain to help increase clinical certainty of diagnosis.

One of the theories that explain the onset and progress of AD, according to neuroscientists and clinicians, is the amyloid-beta (Aβ) phenomenon, also known as the amyloid hypothesis. It is one of the lesions that define the neuropathology of AD due to how extracellular plaques in the brain are built by the dyshomeostasis between the production and clearance of Aβ₄₂ and consequent neuritic and glial cytopathology in memory and cognitive sections of the brain [12, 13].

The second brain lesion of AD is neurofibrillary tau protein tangles [14]. The phenomena of aggregated hyperphosphorylated tau proteins are also regarded as the tau tangles hypothesis. It is known that amyloid-beta (Aβ) plaques play a central role in the risk and progress of AD, while the number of neurofibrillary tangles (NFTs) correlates with the degree of dementia more strongly than the number of plaques [15].

Amyloid-beta (Aβ) and tau proteins’ associations with AD are the focus of several biological studies and research. Other subjects of research are APOE4, cerebrospinal fluid (CSF), and non-CSF body fluids (such as saliva, serum, and urine). Data and results obtained from the research are either used to develop diagnostic models [16, 17] or drugs [18].

The time factor hypothesis was developed in response to the urgent need for timely medical intervention for AD based on accurate diagnostics. This article consists of four sections: a review of mathematical, emerging tech models and other results (Section 2), the time factor hypothesis (Section 3), a summative discussion (Section 4), and the conclusion (Section 5).

In this section, we will review some mathematical models of AD, followed by a survey of parameters and premixes of emerging technologies and other studies in the subject’s context. We will explore various mathematical models of AD, such as the amyloid hypothesis, tau hypothesis, and neuroinflammation hypothesis, which help us understand the underlying mechanisms of the disease, as well as identify caveats to support the time factor hypothesis vis-`a-vis critical factors of AD, AD pathogenesis, onset and progression of AD. Additionally, we will examine the use of various parameters and premixes in emerging technologies and other studies, such as machine learning algorithms and neuro-imaging, along with autopsy findings on the aging brain, brain weight loss and aging, and brain atrophy to gain insights into general, early, and timely interventions.

2.1 Mathematical models of AD
Models are optimized designs of solutions to diverse real-life problems. Researchers have developed mathematical models to define critical components/factors of AD [18], its pathogenesis [19], onset and progression [20], and many more. These models aim to provide a deeper understanding of the neuropathogenesis of AD, including the molecular and cellular processes that lead to it, drug development, and simulation.
Mathematical models could be designed to focus on various aspects of AD, such as the amyloid-β aggregation process [21, 22] in the presence of metal ions [23], the survey of amyloid-β and tau protein-dependent pathologies [24], brain atrophy from tau pathology [25], vagus nerve stimulation [26], protein misfolding mechanisms in neurological diseases [27], etc.
These models agree on the concept and use of parameters related to the death of neurons, homeostasis, and imbalance of glial cells in the central nervous system (CNS), i.e., astroglia and microglia activities about the production, clearance, diffusion, and agglomeration of amyloid proteins.
In the context of this article, we will take a closer look at three mathematical models presented by Hao et al. [18], Puri et al. [19], and Bertsch et al. [20]. These models provide insights into AD’s onset, progression, and underlying bio-molecular mechanisms.

2.1.1 List of selected parameters
A point x in cerebral tissue (Ω), u_m (x,s) molar concentration of Aβ polymer of length m at point x and time (s) in hours, 1 ≤ m < N, surviving and dead neurons N_s and N_d, quiescent and proliferating astroglia A_q and A_p, reactive and normal microglia M₁ and M₂, diffusion d, agglomeration rate (a), reactive oxidative stress R, Aβ release rate
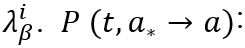 probability for neuron (a) to jump from state a_* to state a ∈ [0, 1].

2.1.2 Critical factors of AD
Hao et al. [18] proposed a mathematical model for AD that takes into account critical variables associated with the disease. Their model includes neurons, astrocytes, microglia, peripheral macrophages, amyloid β aggregation, and hyperphosphorylated tau proteins. The authors utilized systems of partial differential equations to represent the interactions between these variables in the context of AD.
The model provides a quantitative framework for studying the dynamics of AD by capturing the complex interplay between different factors contributing to the development and progression of AD. The simulation of the model was utilized to test the efficacy of drugs that either failed in clinical trials or are currently in clinical trials. A unique analogy from Hao et al. [18] is that the decay (partial derivative) of any of the factors can be represented by the following equation:

[factor decay] = [production] — [degradation]

While the accumulation of say, amyloid-β peptide satisfies:

[accumalation rate] = [production] — [clearance]

For further information, please refer to the article. However, it’s worth noting that while the model effectively captures the current state of AD, it doesn’t include parameters to identify the history or predict the progression of the disease. This highlights the urgent need for a hypothesis for timely interventions.

2.1.3 AD pathogenesis
Puri et al. [19] developed a mathematical model that shares similarities with the model proposed by Hao et al. [18]. Both models define critical components of AD pathogenesis based on differential rate equations. We note, as with the remarks made regarding Hao et al. [18], that research goals, drugs, and other mechanisms have failed over the decades because they focused on managing the aftermath of the disease rather than addressing the core problem.

2.1.4 Onset and progression of AD

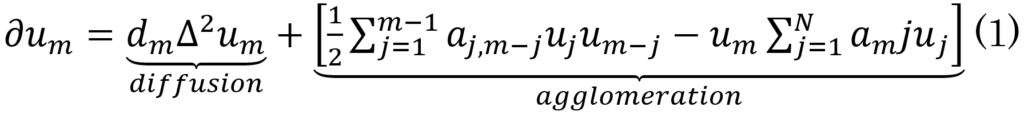
Bertsch et al. [20] model (Eq. 1) describes the onset of AD due to the variation of the molar concentration of oligomeric AB₄₂ polymers based on diffusion and agglomeration rates at a point x ∈ Ω over a short time, i.e.,

[variation in (short) time] = [diffusion] + [agglomeration]

The concentration of AB₄₂ at x ∈ Ω at a specific time s as a result of production and the in+out flow is expected to be small owing to the small diffusion coefficient d_m when m is large, as big assemblies of monomers do not move (i.e., U_N,N = 0). However, this equilibrium is highly volatile, so it is easily triggered by source factors (Ƒ), such as coagulation. Thus, Eq.1 becomes Eq.2. This leads to diffusion being equal to zero in addition to AB₄₂ production in the brain.

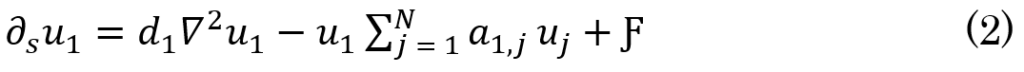
As a result, a transitive relationship between diffusion (and production), fibrils activities, oligomers formulation, and plaques development can be deduced based on the increase in the production level of monomers, which implies an increase in polymer length from 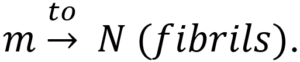This, in turn, leads to the creation of oligomers, which leads to the formation of plaques. The authors modeled the progression of AD using the function f(x,a,t)da, which expresses the degree of malfunctioning neurons with parameter a ranging from 0 to 1 at a time (t). Furthermore, over time, the malfunctioning leads to the deterioration of neurons with a rate of v = v(x,a,t). Therefore, the progression of the disease can be defined by

J[f] = ∂_tf + ∂_a(f(v)[f])

where

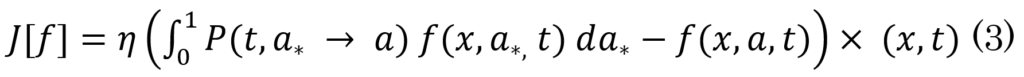
and

otherwise

Please refer to Bertsch et al. [20] for more detailed information about this model. It is important to note, however, that this model does not indicate the timing of any of these activities concerning age.

2.1.5 Observations

In summary of the above models, key observations are:

1. Although time is a critical parameter in all of the models, their longitudinal consideration of time’s integral effect on the onset of AD is often downplayed or overlooked.
2. The models lack a consistent or standard rate to promptly deduce the individualized effect of the disease or history.
3. The models’ outcomes are not generalizable to younger adults as they are based on the assumption that age is above 65 years.

2.2 Emerging technologies
As earlier indicated, there are no diagnostic tools for AD, and methodologies that exist generate only partial diagnostics of the disease. This further exacerbates issues concerning AD. For one, patients cannot be moved into the treatment phase without a diagnosis, giving the disease more time to cause intense atrophy. Emerging technologies, empowered by ubiquitous computing, are being employed to find solutions to the health problems constituted by AD. In this section, we highlight the advances made under two subjects: machine learning and neuroimaging.

2.2.1 Machine learning algorithms
Regarding the context and subject, defining the data acquisition pipeline is herculean as it demands the input of several experts. Furthermore, neuroscientists, bioinformatics, and data scientists (to mention a few) are needed to interpret the data. Samples usually required in such pipelines include most body fluids. Blood, saliva, urine, and CSF are examples. Researchers then develop algorithms (usually) built on mathematical or statistical principles to determine classical patterns in the dataset. Identified patterns are then used to classify cohorts [16, 17] to extend such results to the clinical diagnoses of AD.

2.2.2 Neuroimaging
Neuroimaging is taking functional or structural picture images of the brain. The most common types of neuroimaging are computerized axial tomography (CAT), magnetic resonance imaging (MRI), positron emission tomography (PET), and functional magnetic resonance imaging (fMRI). CAT and MRI are structure imaging, while PET and fMRI produce functional images of the brain. The context of this article does not call for further details of neuroimaging. Suffice it to indicate that neurologists decipher the state of the brain with neuroimages. For example, PET and radioactive tracers have made it possible to detect beta-amyloid in vivo. PET supports the amyloid hypothesis. With this technology, people with cognitive complaints in which AD is a possible diagnosis take the PET scan to detect beta-amyloid plaques and built-ups in the brain. In particular, possible AD dementia is a case where the core criteria for all-cause dementia are met, but the presentation is an atypical course or of mixed etiology [28]. For instance, the impact of normal aging and elderly stage AD are barely distinguishable in neuroimaging [29]. In this case, convolutional neural networks (CNNs) or other machine learning algorithms could be employed to aid in correct prediction, classification, and distinguishing between aging images, early-stage mild cognitive impairment (MCI), and AD [30].

2.3 Other results and studies

2.3.1 Autopsy findings on the aging brain and their relationship to neurodegeneration
Autopsy studies have shown that normal aging is associated with a range of changes in the brain. These changes include the loss of brain weight, the appearance of amyloid bodies, granulovacuolar degeneration (GVD), and Hirano bodies in the hippocampus. These findings indicate neuritic dystrophy, atrophy of the gyri, and widening of sulci, which support the subsequent loss of brain weight due to aging. In addition, amyloid plaques and NFTs, which are known pathological lesions and hallmarks of AD, are also observed in the aging human brain, even in people without dementia.
In addition, studies have shown that individuals with trisomy 21, also known as Down syndrome, have three copies of the APP gene and almost always develop neuropathology characteristics of AD later in life. Even those who do not develop AD and die in their early-to-mid teens from other causes have been found to have abundant diffuse Aβ plaques without neuritic dystrophy, microgliosis, astrocytosis, and tangle formation. These pathological changes would typically accumulate gradually in individuals with trisomy 21 in their late teens and beyond [12].
These findings suggest that the underlying mechanisms of neurodegeneration may begin in the aging brain, even before the onset of clinical symptoms of dementia [31].

2.3.2 Brain weight loss and aging: effects on cognitive functioning
According to Dekaban [32], the weight of a normal brain is between 1200–1400 g. However, the decrease in brain weight typically starts around 45–50 years of age and reaches its lowest value after age 86 years. In their institution, the average brain weight of 100-year-olds was found to be 1097 g (n = 24), and it remained nearly the same (1093 g at 100–111 years old; n = 61) even in cases where the individual is over 100 years old.

This decrease in brain weight is attributed to cerebral atrophy, which implies the loss of brain cells or the number of connections between brain cells. This, in turn, leads to a decline in cognitive functions, such as problems with thinking, memory, multitasking abilities, and other everyday tasks for aging people without dementia [33]. However, even in people without dementia, the aging brain may exhibit pathological lesions, such as amyloid plaques and NFTs, which are known to be the hallmarks of AD [31, 34].

2.3.3 Brain atrophy
Consider Eq. 1 from Bertsch et al. [20] again. The equation models the onset of AD as a result of longitudinal upward variation of the (aggregation) concentration of Aβ m-polymers as a result of reduced diffusion of insoluble fibrils of Aβ and increased coagulation of Aβ monomers into oligomers and subsequently plaques. This assertion critically contributes to the proposed time factor hypothesis, in that, it illuminates the need to determine what age/time this scenario is most likely to commence.

The list of observations in section 2.1.5 is replicated in section 2.3. Neuropathology associated with AD typically begins decades before the onset of clinical symptoms and the manifestation of the disease [35, 36]. Thus, therapeutic interventions targeting the mild-to-moderate clinical stage may be too late to effectively slow or prevent the disease progression [12]. The complex etiology of AD makes it unrealistic to develop drugs capable of reversing decades-long atrophy of nerves, nerve pathways, or autonomous mechanisms. Similarly, it is impossible to resuscitate dead cells, reverse excessive or under-secreted proteins, or re-engineer a broken nervous system.

While age is the most significant known risk factor for AD, not all susceptible aged individuals exhibit features of the disease [37]. Also, there are individuals with early onset of the disease. The time factor hypothesis proposes that focusing on seemingly healthy individuals in research may be essential to reverse the AD epidemic. This approach involves identifying early biomarkers of AD and developing appropriate ‘therapeutic’ interventions that can slow or prevent the disease progression before clinical symptoms become apparent.

3.1 Cognitive function algorithm
Based on the parameters and premises discussed in Section 2, a machine-learning algorithm has been developed. The pseudocode of the algorithm can be found in the supplementary material (Supplementary Material 1). The algorithm defines several functions to check for different aspects of brain health based on the given premises: check brain weight loss (age, brain weight) function checks whether the brain weight is within the normal range for a given age, while the check cognitive decline (age, cognitive functions) function checks whether there are any signs of cognitive decline based on the age and cognitive functions. The check brain lesions (lesions present) function checks whether there are any known pathological lesions in the brain and check neuritic dystrophy (amyloid bodies, GVD, Hirano bodies) function checks for evidence of neuritic dystrophy.
Upon execution, the algorithm calls these functions the assigned sample age X. It then checks and returns different aspects of brain health. See the table for algorithm results with different age values (Table 1).

Age = X	30	40	50	60	70
Brain_weight = ?	1300	1250	1200	1200	1150
Cognitive_functions = ?	Normal	Normal	Normal	Normal	Decline
Lesions_present = ?	False	False	False	True	True
Amyloid_bodies = ?	True	True	True	True	True
GVD = ?	False	True	True	True	True
Hirano_bodies = ?	False	False	True	True	True

Table 1: Results of example usage of the machine learning algorithm for age (X) = 30, 40, 50, 60, and 70. Notice that granulovacuolar degeneration (GVD) is true (already started) at age 40, with normal cognitive functions and false lesions presence. Thus, this suggests that clinical advances in the fight against Alzheimer’s disease may need to be focused on the age group 30–40, where subtle changes related to the disease may already be occurring.

Additionally, a logistic regression model was created and trained to predict using the data (Table 1) generated by the machine learning algorithm. The pseudocode for the logistic regression can be found in the supplementary material (Supplementary Material 2). The logistic regression model was then used to predict the likelihood of AD for individuals with ages 30, 40, 50, 60, and 70 while assuming a brain weight of 1300. The results indicate that:

1. Likelihood of AD for age 30: 0.52%
2. Likelihood of AD for age 40: 4.02%
3. Likelihood of AD for age 50: 20.31%
4. Likelihood of AD for age 60: 61.53%
5. Likelihood of AD for age 70: 92.48%

Based on the results, the likelihood of AD increases with age. Notably, GVD is present at age 40, indicating that changes related to AD may already be occurring at that age. However, normal cognitive functions and the false lesions presence suggest that the patient is not yet exhibiting significant symptoms of AD. This finding emphasizes the need for the pivotal consideration of the integral effect of time on the onset of AD, which is usually downplayed in studies and models. Furthermore, this finding suggests that clinical advancements in the fight against AD may need to be focused on the age group of 30–40, where subtle changes related to the disease may already be occurring.

Our findings also indicate that an average healthy individual experiences a brain weight loss of around 4 g per year, even without dementia. This is based on the assumption that the average age and brain weight of a healthy individual is 47 years and 1300 g, respectively. Also, it is assumed that the brain weight decreases to 1095 g at 105 years, resulting in a loss of 205 g over 58 years. This rate of brain weight loss is more aggressive and higher for individuals with AD, which is estimated to cause a 10% faster rate of brain atrophy compared to the normal aging process [38].

To further support this conclusion, we simulated mathematical models Eq.1 for the aggregation of Aβ from Bertsch et al. [20] and re-interpreted Figure 6 [39] using a brain weight loss rate of 4 g per year (y-axis) and time (decades) on the x-axis (Figure 1). Our attention is directed to the points with red marks for the results of the simulations. The grid allows the ease to count in decades on the x-axis and shows consistency with our conclusions: a) the average healthy adult experiences a brain weight loss of approximately 4 g per year, and b) the 30–40 age bracket should be a key area of focus for clinical advances in the battle against AD. If the total effect (weight loss) by the brain due to age and Aβ₄₂ plaques is equal to or below 4 g (red mark on the y-axis), the individual is normal. An individual is at risk if the level of CSF Aβ, CSF tau, or amyloid PET count is otherwise or higher concerning age. GVD is also observed at age 40 (red mark on the x-axis). Brain weight or size is critical in this analogy as it indicates the buoyancy of the brain. Anyaiwe [40] proposed the use of brain size for diagnosing AD.

Figure 1: A grid-aided interpretation of Figure 6 [39] using a brain weight loss rate of 4 g per year (y-axis) and time (decades) on the x-axis. If the total effect (weight loss) by the brain due to age and Aβ₄₂ plaques is equal to or below 4 g (red mark on the y-axis), the individual is normal. An individual is at risk if the level of CSF Aβ, CSF tau, or amyloid PET count is otherwise concerning age. Granulovacuolar degeneration (GVD) is observed at age 40 (red mark on the x-axis).

This study aims to show that time is of critical essence in the science of timely diagnosis and care for AD patients. Essentially, earlier intervention gives a wider scope for help and possible interventions even before signs of the disease onset. These interventions could be in many aspects. For example, maintaining CSF Aβ₄₂ secretion level (maybe through medication or diet) or enhancing its diffusion has been found to collaborate with brain global atrophy.

We observed (as evident in the mathematical models reviewed in the course of this article) that time is not considered in its present term, nor is the integral effect of the disease over time viewed as a vital component in the science of Alzheimer’s. Rather, time is used in retrospect as in the age of the individual with a hinge on the state of the manifestations of the disease. The time factor hypothesis is the tool to reverse this practice.

“Recent data in individuals with familial AD (i.e., individuals with rare genetic mutations that develop AD) has shown that beta-amyloid can begin to accumulate 20–25 years before the clinical onset of the disease” [41]. However, it appears that this observation has been overlooked. Only by developing a time factor hypothesis can researchers refocus their aims. Similar oversights are also obtainable in adopting modern technologies and machine learning algorithms in discovering AD biomarkers or classification models, which, by extension, support the long list of failed drugs.

In this article, we showed that Aβ₄₂ aggregation starts around the age of 30–40 years. With this information, we propose the need to re-engineer the concepts of the science of AD. The number of AD patients will experience a nose dive if effort aimed at timely prevention of (for instance) Aβ₄₂ aggregation is expended.

We suggest creating age-stratified datasets and utilizing machine learning techniques in future work. Specifically, age brackets of 30–39, 40–49, and 50–59 should be generated to capture distinctive behavioral patterns and compare them with those of an aged control group (aged 60 years and older).

No human consent is necessary.

No funding was available.

The authors declare that they have no conflict of interest.

The supplementary material for this article can be found online at: https://seriesscience.com/wp-content/uploads/2023/12/Supplementary-Material.pdf.

1. Sosa-Ortiz AL, Acosta-Castillo I, Prince MJ. Epidemiology of dementias and Alzheimer’s disease. Arch Med Res. 2012;43(8):600-08.
2. National Institutes of Aging. Alzheimer’s and dementia. 2022.
3. Alzheimer’s Association. Alzheimer’s and Dementia. 2022.
4. Wilson RS, Barral S, Lee JH, et al. Heritability of different forms of memory in the Late Onset Alzheimer’s Disease Family Study. J Alzheimers Dis. 2011;23(2):249-55.
5. National Institutes of Aging. Alzheimer’s Disease Genetics Fact Sheet. 2022.
6. Zanetti O, Solerte SB, Cantoni F. Life expectancy in Alzheimer’s disease (AD). Arch Gerontol Geriatr. 2009;49 Suppl 1:237-43.
7. Dhana K, Franco OH, Ritz EM, et al. Healthy lifestyle and life expectancy with and without Alzheimer’s dementia: population based cohort study. BMJ. 2022;377:e068390.
8. Alothman D, Card T, Lewis S, et al. Risk of Suicide After Dementia Diagnosis. JAMA Neurol. 2022;79(11):1148–154.
9. Cummings J, Lee G, Zhong K, et al. Alzheimer’s disease drug development pipeline: 2021. Alzheimers Dement. 2021;7(1):e12179.
10. James C, Ranson JM, Everson R, et al. Performance of Machine Learning Algorithms for Predicting Progression to Dementia in Memory Clinic Patients. JAMA Netw Open. 2021;4(12):e2136553.
11. Li R, Wang X, Lawler K, et al. Applications of artificial intelligence to aid early detection of dementia: A scoping review on current capabilities and future directions. J Biomed Inform. 2022;127:104030.
12. Selkoe DJ, Hardy J. The amyloid hypothesis of Alzheimer’s disease at 25 years. EMBO Mol Med. 2016;8(6):595-608.
13. Walker LC. Aβ plaques. Free Neuropathology. 2020;1(2020):1-42.
14. Long JM, Holtzman DM. Alzheimer Disease: An Update on Pathobiology and Treatment Strategies. Cell. 2019;179(2):312-39.
15. Walsh DM, Selkoe DJ. Amyloid β-protein and beyond: the path forward in Alzheimer’s disease. Curr Opin Neurobiol. 2020;61:116-24.
16. Anyaiwe DEO, George WD, Singh GB. Classification by Clustering: Saliva MS-SELDI Data for Alzheimer’s Disease Diagnosis. 2017 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC). 2017:92-97.
17. Anyaiwe DEO, Singh GB, Wilson GD, et al. Computational Convolution of SELDI Data for the Diagnosis of Alzheimer’s Disease. High Throughput. 2018;7(2):14.
18. Hao W, Friedman A. Mathematical model on Alzheimer’s disease. BMC Syst Biol. 2016;10(1):108.
19. Puri IK, Li L. Mathematical modeling for the pathogenesis of Alzheimer’s disease. PLoS One. 2010;5(12):e15176.
20. Bertsch M, Franchi B, Marcello N, et al. Alzheimer’s disease: a mathematical model for onset and progression. Math Med Biol. 2017;34(2):193-214.
21. Dayeh MA, Livadiotis G, Elaydi S. A discrete mathematical model for the aggregation of β-Amyloid. PLoS One. 2018;13(5):e0196402.
22. Chen CY, Tseng YH, Ward JP. A mathematical model demonstrating the role of interstitial fluid flow on the clearance and accumulation of amyloid β in the brain. Math Biosci. 2019;317:108258.
23. Asili E, Yarahmadian S, Khani H, et al. A Mathematical Model for Amyloid-𝜷 Aggregation in the Presence of Metal Ions: A Timescale Analysis for the Progress of Alzheimer Disease. Bull Math Biol. 2019;81(6):1943-964.
24. Vosoughi A, Sadigh-Eteghad S, Ghorbani M, et al. Mathematical Models to Shed Light on Amyloid-Beta and Tau Protein Dependent Pathologies in Alzheimer’s Disease. Neuroscience. 2020 ;424:45-57.
25. Schafr A, Chaggar P, Thompson TB, et al. Predicting brain atrophy from tau pathology: a summary of clinical findings and their translation into personalized models. Brain Multiphysics. 2021;2:100039.
26. Miranda J. A Mathematical Model of Vagus Nerve Stimulation in Alzheimer’s Disease. 2022.
27. Carbonell F, Iturria-Medina Y, Evans AC. Mathematical Modeling of Protein Misfolding Mechanisms in Neurological Diseases: A Historical Overview. Front Neurol. 2018;9:37.
28. Johnson KA, Minoshima S, Bohnen NI, et al. Update on appropriate use criteria for amyloid PET imaging: dementia experts, mild cognitive impairment, and education. Amyloid Imaging Task Force of the Alzheimer’s Association and Society for Nuclear Medicine and Molecular Imaging. Alzheimers Dement. 2013; 9(4): e106-9.
29. Vemuri P, Lesnick TG, Przybelski SA, et al. Age, vascular health, and Alzheimer disease biomarkers in an elderly sample. Ann Neurol. 2017;82(5):706-18.
30. Janghel RR, Rathore YK. Deep Convolution Neural Network Based System for Early Diagnosis of Alzheimer’s Disease. IRBM. 2021;42(4):258-67.
31. Sengoku R. Aging and Alzheimer’s disease pathology. Neuropathology. 2020;40(1):22-9.
32. Dekaban AS. Changes in brain weights during the span of human life: relation of brain weights to body heights and body weights. Ann Neurol. 1978;4(4):345-56.
33. Zanto TP, Gazzaley A. Aging of the frontal lobe. Handb Clin Neurol. 2019;163:369-89.
34. Serrano-Pozo A, Mielke ML, Muzitansky A, et al. Stable size distribution of amyloid plaques over the course of Alzheimer disease. J Neuropathol Exp Neurol. 2012;71(8):694-01.
35. Bateman RJ, Munsell LY, Morris JC, et al. Human amyloid-beta synthesis and clearance rates as measured in cerebrospinal fluid in vivo. Nat Med. 2006;12(7):856-61.
36. Villemagne VL, Burnham S, Bourgeat P, et al. Amyloid β deposition, neurodegeneration, and cognitive decline in sporadic Alzheimer’s disease: a prospective cohort study. Lancet Neurol. 2013;12(4):357-67.
37. National Institutes of Aging. What Causes Alzheimer’s Disease? 2019.
38. Kennard C. Four Key Changes in the Alzheimer’s Brain. 2014.
39. Jack CR Jr, Knopman DS, Jagust WJ, et al. Tracking pathophysiological processes in Alzheimer’s disease: an updated hypothetical model of dynamic biomarkers. Lancet Neurol. 2013;12(2):207-16.
40. Anyaiwe OED. P4-264: Pathology & Neuroimaging for Alzheimer’s disease. Alzheimers Dement. 2019;15(7): 1382-1382.
41. Bateman RJ, Xiong C, Benzinger TL, et al. Clinical and biomarker changes in dominantly inherited Alzheimer’s disease. N Engl J Med. 2012;367(9):795-804.